Interfaces superfluide-solide avec couplage de modes
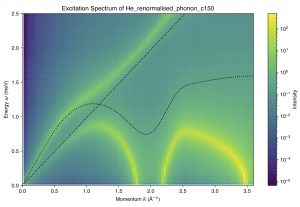 Nous étudions comment les modes collectifs d’un superfluide (phonons, modes de Bogolioubov, rotons) s’hybrident avec les modes de surface d’un solide (par exemple des phonons acoustiques) et comment ce couplage induit par les fluctuations reconfigure la physique interfaciale. Un recouvrement spectral adéquat renormalise la réponse de surface des deux milieux, peut adoucir la branche superfluide au voisinage de la paroi et déclencher une instabilité vers une phase supersolide à modulation de densité. Côté transport, le même couplage engendre un frottement quantique entre un super-écoulement et le solide, régi par un critère de Landau interfacial qui fixe les conditions d’apparition de la dissipation. En ajustant paramètres des matériaux et l’intensité du couplage, on développe l’ingénierie des interfaces superfluide-solide.
Nous étudions comment les modes collectifs d’un superfluide (phonons, modes de Bogolioubov, rotons) s’hybrident avec les modes de surface d’un solide (par exemple des phonons acoustiques) et comment ce couplage induit par les fluctuations reconfigure la physique interfaciale. Un recouvrement spectral adéquat renormalise la réponse de surface des deux milieux, peut adoucir la branche superfluide au voisinage de la paroi et déclencher une instabilité vers une phase supersolide à modulation de densité. Côté transport, le même couplage engendre un frottement quantique entre un super-écoulement et le solide, régi par un critère de Landau interfacial qui fixe les conditions d’apparition de la dissipation. En ajustant paramètres des matériaux et l’intensité du couplage, on développe l’ingénierie des interfaces superfluide-solide.
Références:
Voir le résumé (en anglais)
Supersolidity, combining superfluid and crystalline orders, has been realized in dipolar Bose-Einstein condensates by tuning interatomic interactions. Here we show that supersolidity can also emerge from mode coupling at a superfluid-solid interface, without modifying bulk interactions and for a broad class of superfluids. Using an analytical and numerical treatment of the coupled superfluid and phonon fields, we derive the criterion for a density-modulation instability driven by interfacial coupling and dependent on dimensionality. In superfluid helium, the instability first appears at the roton mode, while in a Bose-Einstein condensate with contact interactions it occurs at the lowest accessible wave vector set by the system size. Beyond the threshold, the ground state acquires an interfacial density modulation while the bulk remains superfluid, forming a hybrid superfluid-supersolid phase. Our results identify interfacial mode coupling as a promising route to supersolidity, enabling the simultaneous exploitation of interfacial supersolid and bulk superfluid quantum properties.
Transport nanofluidique non linéaire et fluctuant
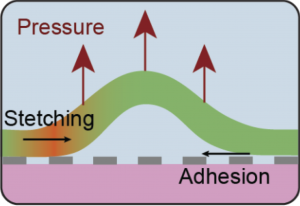 Le transport nanofluidique non linéaire apparaît lorsque l’interface est rendue spatialement inhomogène ou mécaniquement déformable. Côté électrocinétique, des gradients de nombre de Dukhin (motifs de charge de surface, de glissement et de conduction de surface) décrits dans le formalisme de Poisson–Nernst–Planck produisent rectification, conductance dépendante de la pression et fortes réponses réglables qui servent de sondes de l’interface solide–liquide confinée. Côté mécanique, les solides ont des fluctuations à des fréquences hydrodynamiques conduisant à des couplages subtiles, tandis que de fortes chutes de pression et contraintes à l’échelle nanométrique déforment les canaux, engendrant seuils, hystérésis et comportement memristif. Ces non-linéarités permettent d’améliorer le transport hydrodynamique, de développer des memristors ioniques et, plus largement, d’affiner la compréhension expérimentale fondamentale du transport nanofluidique.
Le transport nanofluidique non linéaire apparaît lorsque l’interface est rendue spatialement inhomogène ou mécaniquement déformable. Côté électrocinétique, des gradients de nombre de Dukhin (motifs de charge de surface, de glissement et de conduction de surface) décrits dans le formalisme de Poisson–Nernst–Planck produisent rectification, conductance dépendante de la pression et fortes réponses réglables qui servent de sondes de l’interface solide–liquide confinée. Côté mécanique, les solides ont des fluctuations à des fréquences hydrodynamiques conduisant à des couplages subtiles, tandis que de fortes chutes de pression et contraintes à l’échelle nanométrique déforment les canaux, engendrant seuils, hystérésis et comportement memristif. Ces non-linéarités permettent d’améliorer le transport hydrodynamique, de développer des memristors ioniques et, plus largement, d’affiner la compréhension expérimentale fondamentale du transport nanofluidique.
Références:
Voir le résumé (en anglais)
Nanofluidic memristors promise brain-inspired information processing with ions, yet their microscopic origin remains debated. So far, ionic memory has been attributed to ion-specific interactions, dynamic wetting, chemical reactions or mechanical deformations, yet typically without direct evidence. Here, by combining operando interferometric imaging with electrokinetic measurements, we directly visualize voltage-induced blistering of the confining walls of two-dimensional (2D) nanochannels, as key origin of memristive hysteresis. We identify two distinct classes of blisters: unidirectional, driven by electrostatic forces on surface charges, and bidirectional, arising from osmotic pressure due to concentration polarization. This mechanistic framework explains device evolution and device-to-device variability, and reframes stochastic blistering as a functional design element. Our results constitute a direct proof of electromechanical coupling as a robust pathway to ionic memory in 2D nanochannels and open routes toward high-performance ionic memristors and electrically actuated nanofluidic valves.
Voir le résumé (en anglais)
In this paper we examine how porosity fluctuations affect the hydrodynamic permeability of a porous matrix or membrane. We introduce a fluctuating Darcy model, which couples the Navier-Stokes equation to the space- and time-dependent porosity fluctuations via a Darcy friction term. Using a perturbative approach, a Dyson equation for hydrodynamic fluctuations is derived and solved to express the permeability in terms of the matrix fluctuation spectrum. Surprisingly, the model reveals strong modifications of the fluid permeability in fluctuating matrices compared to static ones. Applications to various matrix excitation models – breathing matrix, phonons, active forcing – highlight the significant influence of matrix fluctuations on fluid transport, offering insights for optimizing membrane design for separation applications.
Transport nanofluidique couplé aux électrons
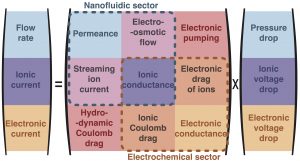 Les effets croisés aux interfaces sont déterminants en nanofluidique : à ces échelles, l’interface permet de coupler entre transport de charge, de matière et de chaleur au sein d’un électrolyte. Nous allons plus loin en couplant ces transports aux électrons du solide et donc à la conductivité électronique. Cela est possible directement via l’interaction coulombienne entre les ions et les électrons ou via des couplages induits par les fluctuations. Ainsi, ces couplages croisés permettent de nouveaux types de dispositifs nanofluidiques : générateurs hydroélectriques nanométriques convertissant des écoulements visqueux en courant, transfert d’écoulement à travers des parois minces pour connectant des canaux, augmentation contrôlée de la conductivité ionique et de la perméabilité hydrauliques, et pilotage actif des écoulements par un signal électrique (et réciproquement).
Les effets croisés aux interfaces sont déterminants en nanofluidique : à ces échelles, l’interface permet de coupler entre transport de charge, de matière et de chaleur au sein d’un électrolyte. Nous allons plus loin en couplant ces transports aux électrons du solide et donc à la conductivité électronique. Cela est possible directement via l’interaction coulombienne entre les ions et les électrons ou via des couplages induits par les fluctuations. Ainsi, ces couplages croisés permettent de nouveaux types de dispositifs nanofluidiques : générateurs hydroélectriques nanométriques convertissant des écoulements visqueux en courant, transfert d’écoulement à travers des parois minces pour connectant des canaux, augmentation contrôlée de la conductivité ionique et de la perméabilité hydrauliques, et pilotage actif des écoulements par un signal électrique (et réciproquement).
Références:
Voir le résumé (en anglais)
The transport properties of nanofluidic channels are usually studied under constant (DC) voltage or pressure driving. However, the frequency response under sinusoidal (AC) drivings offers rich insights into the time-dependent transport mechanisms. Inspired by recent electrochemical approaches, we investigate the couplings between ionic and electronic transport under AC driving. We show that conduction electrons of the channel walls participate in ionic current via capacitive electrochemical coupling, defining a critical frequency and length scale where electron-dominated conductivity emerges. We further analyze how electron-ion coupling modifies electro-osmotic flows, and demonstrate that fluctuation-induced momentum transfer between the electrolyte and wall electrons produces distinct AC transport signatures depending on the charge carrier polarity. Altogether, we establish a frequency-dependent transport matrix that couples ionic, electronic and hydrodynamic flows. These findings establish AC nanofluidic transport as a powerful probe of interfacial phenomena under confinement, and suggest new directions for engineering nanofluidic functionalities through electron-electrolyte coupling.
Voir le résumé (en anglais)
The world of nanoscales in fluidics is the frontier where the continuum of fluid mechanics meets the atomic, and even quantum, nature of matter. While water dynamics remains largely classical under extreme confinement, several experiments have recently reported coupling between water transport and the electronic degrees of freedom of the confining materials. This avenue prompts us to reconsider nanoscale hydrodynamic flows under the perspective of interacting excitations, akin to condensed matter frameworks. Here we show, using a combination of many-body theory and molecular simulations, that the flow of a liquid can induce the flow of another liquid behind a separating wall, at odds with the prediction of continuum hydrodynamics. We further show that the range of this ‘flow tunnelling’ can be tuned through the solid’s electronic excitations, with a maximum occurring when these are at resonance with the liquid’s charge density fluctuations. Flow tunnelling is expected to play a role in global transport across nanoscale fluidic networks, such as lamellar graphene oxide or MXene membranes. It further suggests exploiting the electronic properties of the confining walls for manipulating liquids via their dielectric spectra, beyond the nature and characteristics of individual molecules.
Voir le résumé (en anglais)
Hydraulic energy is a key component of the global energy mix, yet there exists no practical way of harvesting it at small scales, from flows with low Reynolds number. This has triggered a search for alternative hydroelectric conversion methodologies, leading to unconventional proposals based on droplet triboelectricity, water evaporation, osmotic energy, or flow-induced ionic Coulomb drag. Yet, these approaches systematically rely on ions as intermediate charge carriers, limiting the achievable power density. Here, we predict that the kinetic energy of small-scale “waste” flows can be directly and efficiently converted into electricity thanks to the hydroelectronic drag effect, by which an ion-free liquid induces an electronic current in the solid wall along which it flows. This effect originates in the fluctuation-induced coupling between fluid motion and electron transport. We develop a nonequilibrium thermodynamic formalism to assess the efficiency of such hydroelectric energy conversion, dubbed hydronic energy. We find that hydronic energy conversion is analogous to thermoelectricity, with the efficiency being controlled by a dimensionless figure of merit. However, in contrast to its thermoelectric analogue, this figure of merit combines independently tunable parameters of the solid and the liquid, and can thus significantly exceed unity. Our findings suggest strategies for blue energy harvesting without electrochemistry, and for waste flow mitigation in membrane-based filtration processes.
Frottement solide-liquide induit par les fluctuations
 Le transport nanofluidique est gouverné par le glissement — c’est-à-dire le frottement solide–liquide — qui dépend non seulement de la mouillabilité ou de la chimie de surface, mais aussi de couplages induits par les fluctuations à l’interface. Les fluctuations du liquide (densité moléculaire, charge ionique) se couplent aux excitations internes du solide (électrons, phonons, plasmons), si bien que le frottement interfacial et le glissement reflètent un recouvrement spectral des modes entre liquide et paroi. En ajustant les propriétés du liquide, le confinement ou la réponse du matériau, on peut amplifier ou réduire le glissement de plusieurs ordres de grandeur. Le couplage est bidirectionnel : des fluctuations du liquide peuvent pousser le solide hors de l’équilibre, générant des vents de phonons et des courants électroniques, tandis que les champs fluctuants du solide exercent une rétroaction qui renormalise le frottement. Au total, il en résulte une traînée coulombienne nanofluidique : un coefficient de transport croisé reliant l’écoulement hydrodynamique au transport électronique, ouvrant la voie à des canaux à faible friction et à la conversion d’énergie interfaciale.
Le transport nanofluidique est gouverné par le glissement — c’est-à-dire le frottement solide–liquide — qui dépend non seulement de la mouillabilité ou de la chimie de surface, mais aussi de couplages induits par les fluctuations à l’interface. Les fluctuations du liquide (densité moléculaire, charge ionique) se couplent aux excitations internes du solide (électrons, phonons, plasmons), si bien que le frottement interfacial et le glissement reflètent un recouvrement spectral des modes entre liquide et paroi. En ajustant les propriétés du liquide, le confinement ou la réponse du matériau, on peut amplifier ou réduire le glissement de plusieurs ordres de grandeur. Le couplage est bidirectionnel : des fluctuations du liquide peuvent pousser le solide hors de l’équilibre, générant des vents de phonons et des courants électroniques, tandis que les champs fluctuants du solide exercent une rétroaction qui renormalise le frottement. Au total, il en résulte une traînée coulombienne nanofluidique : un coefficient de transport croisé reliant l’écoulement hydrodynamique au transport électronique, ouvrant la voie à des canaux à faible friction et à la conversion d’énergie interfaciale.
Références:
Voir le résumé (en anglais)
The fundamental understanding of friction of liquids on solid surfaces remains one of the key knowledge gaps in the transport of fluids. While the standard perspective emphasizes the role of wettability and commensurability, recent works have unveiled the crucial role of the solid’s internal excitations, whether electronic or phononic, on liquid-solid dissipation. In this work, we take advantage of the considerable variation of the molecular timescales of supercooled glycerol under mild change of temperature, in order to explore how friction depends on the liquid’s molecular dynamics. Using a dedicated tuning-fork-based AFM to measure the hydrodynamic slippage of glycerol on mica, we report a 2-order of magnitude increase of the slip length with decreasing temperature by only 30°C. However the solid-liquid friction coefficient is found to be a non monotonous function of the fluid molecular relaxation rate, the alpha frequency, at odd with an expected Arrhenius behavior. In particular, the linear increase of friction with the liquid molecular rate measured at high temperature cannot be accounted for by existing modelling. We show that this unconventional and non-arrhenian friction is consistent with a contribution of the solid’s phonons to the liquid-solid friction. This dynamical friction opens new perspectives to control hydrodynamic flows by properly engineering phononic and electronic excitation spectra in channel walls.
Voir le résumé (en anglais)
Nanoscale fluid transport is typically pictured in terms of atomic-scale dynamics, as is natural in the real-space framework of molecular simulations. An alternative Fourier-space picture, that involves the collective charge fluctuation modes of both the liquid and the confining wall, has recently been successful at predicting new nanofluidic phenomena such as quantum friction and near-field heat transfer, that rely on the coupling of those fluctuations. Here, we study the charge fluctuation modes of a two-dimensional (planar) nanofluidic channel. Introducing confined response functions that generalize the notion of surface response function, we show that the channel walls exhibit coupled plasmon modes as soon as the confinement is comparable to the plasmon wavelength. Conversely, the water fluctuations remain remarkably bulk-like, with significant confinement effects arising only when the wall spacing is reduced to 7 Å. We apply the confined response formalism to predict the dependence of the solid-water quantum friction and thermal boundary conductance on channel width for model channel wall materials. Our results provide a general framework for Coulomb interactions of fluctuating matter in nanoscale confinement.
Voir le résumé (en anglais)
An electronic current driven through a conductor can induce a current in another conductor through the famous Coulomb drag effect. Similar phenomena have been reported at the interface between a moving fluid and a conductor, but their interpretation has remained elusive. Here, we develop a quantum-mechanical theory of the intertwined fluid and electronic flows, taking advantage of the non-equilibrium Keldysh framework. We predict that a globally neutral liquid can generate an electronic current in the solid wall along which it flows. This hydrodynamic Coulomb drag originates from both the Coulomb interactions between the liquid’s charge fluctuations and the solid’s charge carriers, and the liquid-electron interaction mediated by the solid’s phonons. We derive explicitly the Coulomb drag current in terms of the solid’s electronic and phononic properties, as well as the liquid’s dielectric response, a result which quantitatively agrees with recent experiments at the liquid-graphene interface. Furthermore, we show that the current generation counteracts momentum transfer from the liquid to the solid, leading to a reduction of the hydrodynamic friction coefficient through a quantum feedback mechanism. Our results provide a roadmap for controlling nanoscale liquid flows at the quantum level, and suggest strategies for designing materials with low hydrodynamic friction.
Voir le résumé (en anglais)
The interface between a liquid and a solid is the location of plethora of intrincate mechanisms at the nanoscale, at the root of their specific emerging properties in natural processes or technological applications. However, while the structural properties and chemistry of interfaces have been intensively explored, the effect of the solid-state electronic transport at the fluid interface has been broadly overlooked up to now. It has been reported that water flowing against carbon-based nanomaterials, such as carbon nanotubes or graphene sheets , does induce electronic currents, but the mechanism at stake remains controversial. Here, we unveil the molecular mechanisms underlying the hydro-electronic couplings by investigating the electronic conversion under flow at the nanoscale. We use a tuning fork-Atomic Force Microscope (AFM) to deposit and displace a micrometric droplet of both ionic and non- ionic liquids on a multilayer graphene sample, while recording the electrical current across the carbon flake. We report measurements of an oscillation-induced current which is several orders of magnitude larger than previously reported for water on carbon , and further boosted by the presence of surface wrinkles on the carbon layer. Our results point to a peculiar momentum transfer mechanism between fluid molecules and charge carriers in the carbon walls mediated by phonon excitations in the solid. Our findings pave the way for active control of fluid transfer at the nanoscale by harnessing the complex interplay between collective excitations in the solid and the molecules in the fluid.
Mécanique géométrique pour les systèmes dissipatifs
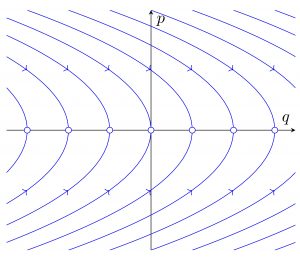 Le cadre de référence pour les dynamiques conservatives est la mécanique hamiltonienne : une structure de Poisson (symplectique) accompagnée d’un hamiltonien. Elle préserve remarquablement les invariants et la structure (symplecticité, Casimirs) et sert de base robuste à l’analyse comme aux intégrateurs géométriques, des particules ponctuelles aux fluides idéaux. Sa limite tient à l’absence d’irréversibilité : dissipation, diffusion et viscosité n’entrent pas dans une évolution purement hamiltonienne. J’étudie des généralisations pour introduire la dissipation sans sacrifier la géométrie. D’abord, des variétés de Poisson singulières — en particulier la géométrie b-symplectique — autorisent des dégénérescences contrôlées le long d’interfaces, ce qui permet, dans certains cas, de retranscrire des effets dissipatifs dans une structure symplectique. Ensuite, l’approche métriplectique/GENERIC ajoute au crochet de Poisson un crochet dissipatif symétriqu semi-positif : l’énergie reste conservée tandis que la production d’entropie est assurée, et, près de l’équilibre, on retrouve la réponse linéaire d’Onsager avec des tenseurs de transport portés directement par le crochet dissipatif. Ensemble, ces outils donnent des modèles thermodynamiquement cohérents pour des systèmes réels, tout en conservant les atouts de la géométrie pour l’analyse et le calcul.
Le cadre de référence pour les dynamiques conservatives est la mécanique hamiltonienne : une structure de Poisson (symplectique) accompagnée d’un hamiltonien. Elle préserve remarquablement les invariants et la structure (symplecticité, Casimirs) et sert de base robuste à l’analyse comme aux intégrateurs géométriques, des particules ponctuelles aux fluides idéaux. Sa limite tient à l’absence d’irréversibilité : dissipation, diffusion et viscosité n’entrent pas dans une évolution purement hamiltonienne. J’étudie des généralisations pour introduire la dissipation sans sacrifier la géométrie. D’abord, des variétés de Poisson singulières — en particulier la géométrie b-symplectique — autorisent des dégénérescences contrôlées le long d’interfaces, ce qui permet, dans certains cas, de retranscrire des effets dissipatifs dans une structure symplectique. Ensuite, l’approche métriplectique/GENERIC ajoute au crochet de Poisson un crochet dissipatif symétriqu semi-positif : l’énergie reste conservée tandis que la production d’entropie est assurée, et, près de l’équilibre, on retrouve la réponse linéaire d’Onsager avec des tenseurs de transport portés directement par le crochet dissipatif. Ensemble, ces outils donnent des modèles thermodynamiquement cohérents pour des systèmes réels, tout en conservant les atouts de la géométrie pour l’analyse et le calcul.
Références:
Voir le résumé (en anglais)
In this article we analyze several mathematical models with singularities where the classical cotangent model is replaced by a b-cotangent model. We provide physical interpretations of the singular symplectic geometry underlying in b-cotangent bundles featuring two models: the canonical (or non-twisted) model and the twisted one. The first one models systems on manifolds with boundary and the twisted model represents Hamiltonian systems where the singularity of the system is in the fiber of the bundle. The twisted cotangent model includes (for linear potentials) the case of fluids with dissipation. We relate the complexity of the fluids in terms of the Reynolds number and the (non)-existence of cotangent lift dynamics. We also discuss more general physical interpretations of the twisted and non-twisted b-symplectic models. These models offer a Hamilton- ian formulation for systems which are dissipative, extending the horizons of Hamiltonian dynamics and opening a new approach to study non-conservative systems.
Voir le résumé (en anglais)
General equations for conservative yet dissipative (entropy producing) extended magnetohydrodynamics are derived from two-fluid theory. Keeping all terms generates unusual cross-effects, such as thermophoresis and a current viscosity that mixes with the usual velocity viscosity. While the Poisson bracket of the ideal version of this model has already been discovered, we determine its metriplectic counterpart that describes the dissipation. This is done using a new and general thermodynamic point of view to derive dissipative brackets, a means of derivation that is natural for understanding and creating dissipative dynamics without appealing to underlying kinetic theory orderings. Finally, the formalism is used to study dissipation in the Lagrangian variable picture where, in the context of extended magnetohydrodynamics, non-local dissipative brackets naturally emerge.