I am theoretical physicist interested in dynamics, condensed matter and statistical physics.
Below are my past and current subjects of research.
Interactions and Dynamics at the Nanoscale Solid-Liquid Interface

At the solid-liquid interface the fluid interacts with both the phonons an the electrons of the solid. These interactions, called respectively phonon drag and Coulomb drag, can only be explained properly using a quantum formalism. While the collisions (generating the phonon drag) are at the origin of the “classical” friction, the coupling between the collective modes of the fluid and the electronic excitations at the surface of the solid (generating the Coulomb drag) are the source of a new kind of friction which is dominant in certain conditions of nanofluidics. In particular, this provides an understanding of the surprising friction in carbon nanotube where the friction drops as the radius is reduced. When imposing a flow, the solid reaches a quasi-equilibrium state where its different quantum particles fulfil a modified fluctuation-dissipation theorem which includes a frequency shift. In particular, we predict the generation of an electric current which has been measured and studied experimentally. The form of the current is tunnable by choosing the internal structure of the solid: this is a quantum effect. Such an flow-induced electric current may have crucial applications if the solid is well engineered: this opens the door to sensing and controlling the flow velocity at the nanoscales and energy production at larger scales. Physically, the liquid exchanges momentum to the phonons and the electrons through respectively the phonon drag and Coulomb drag: this is like a wind blowing on the Fermi sea. In most situations the former is dominant while the latter is negative: this means that the momentum path is from the flow to the phonons, then the electrons and then back to the flow. In pratice this phenomenon reduces the total friction. This opens the door quantum engeenering the friction by controling the internal structure of the solid. Moreover, everything may be affected by confinement, paving the way to new experimental discoveries.
Selected References:
[4] Baptiste Coquinot, Lydéric Bocquet, Nikita Kavokine, Quantum feedback at the solid-liquid interface: flow-induced electronic current and its negative contribution to friction, Physical Review X (2023)Show abstract
An electronic current driven through a conductor can induce a current in another conductor through the famous Coulomb drag effect. Similar phenomena have been reported at the interface between a moving fluid and a conductor, but their interpretation has remained elusive. Here, we develop a quantum-mechanical theory of the intertwined fluid and electronic flows, taking advantage of the non-equilibrium Keldysh framework. We predict that a globally neutral liquid can generate an electronic current in the solid wall along which it flows. This hydrodynamic Coulomb drag originates from both the Coulomb interactions between the liquid’s charge fluctuations and the solid’s charge carriers, and the liquid-electron interaction mediated by the solid’s phonons. We derive explicitly the Coulomb drag current in terms of the solid’s electronic and phononic properties, as well as the liquid’s dielectric response, a result which quantitatively agrees with recent experiments at the liquid-graphene interface. Furthermore, we show that the current generation counteracts momentum transfer from the liquid to the solid, leading to a reduction of the hydrodynamic friction coefficient through a quantum feedback mechanism. Our results provide a roadmap for controlling nanoscale liquid flows at the quantum level, and suggest strategies for designing materials with low hydrodynamic friction.
[3] Mathieu Lizée, Alice Marcotte, Baptiste Coquinot, Nikita Kavokine, Karen Sobnath, Clément Barraud, Ankit Bhardwaj, Boya Radha, Antoine Niguès, Lydéric Bocquet, Alessandro Siria, Strong electronic winds blowing under liquid flows on carbon surfaces, Physical Review X (2023)
Show abstract
The interface between a liquid and a solid is the location of plethora of intrincate mechanisms at the nanoscale, at the root of their specific emerging properties in natural processes or technological applications. However, while the structural properties and chemistry of interfaces have been intensively explored, the effect of the solid-state electronic transport at the fluid interface has been broadly overlooked up to now. It has been reported that water flowing against carbon-based nanomaterials, such as carbon nanotubes or graphene sheets , does induce electronic currents, but the mechanism at stake remains controversial. Here, we unveil the molecular mechanisms underlying the hydro-electronic couplings by investigating the electronic conversion under flow at the nanoscale. We use a tuning fork-Atomic Force Microscope (AFM) to deposit and displace a micrometric droplet of both ionic and non- ionic liquids on a multilayer graphene sample, while recording the electrical current across the carbon flake. We report measurements of an oscillation-induced current which is several orders of magnitude larger than previously reported for water on carbon , and further boosted by the presence of surface wrinkles on the carbon layer. Our results point to a peculiar momentum transfer mechanism between fluid molecules and charge carriers in the carbon walls mediated by phonon excitations in the solid. Our findings pave the way for active control of fluid transfer at the nanoscale by harnessing the complex interplay between collective excitations in the solid and the molecules in the fluid.
Geometric Theory of Mechanics and Thermodynamics
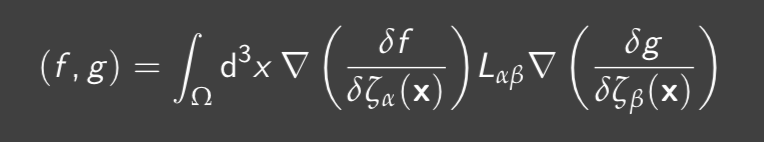
The standard formalism to study dynamics is the Hamiltonian mechanics which is founded on a symplectic form (or Poisson bracket) and a dynamical funtion: the Hamiltonian. Such a formalism is powerful to study the dynamics of point objects and fluids in many physical situations and is well suited for numerial integration. However, Hamiltonian dynamics does not include dissipation and then can only study systems at the thermodynamic equilibrium. Yet, some dissipative models can be written in a Hamiltonian structure using non-standard formulations of the theory. This is, in particular, the case with b-symplectic geometry which allows singularities in the phase space. These situations are fascinating for numerical and mathematical studies of dynamics and applies to basic dissipative systems. Another approach is the metriplectic (or GENERIC) framework, which has been developed to adress the limitations of the standard Hamiltonian methods. In this formalism the symplectic form is completed by a pseudo-Riemannian metric and the free energy is used as the dynamical function. Under reasonable assumptions, the two principles of thermodynamics arise from the geometric structure. Such a formalism is well-suited to study close-to-the-equilibrium systems where the thermodynamics is described by Onsager’s linear response. This applies in particular for the majority of models of fluid dynamics, like Naver-Stokes equations. In these models, the metric (or dissipative bracket) contains the microscopic physics and is the geometric realisation of the Onsager’s transport tensor. It can also be derived as a emerging property form grand deviation theory and kinetic theory.
Selected References:
[2] Baptiste Coquinot, Pau Mir, Eva Miranda, Singular cotangent models and complexity in fluids with dissipation, Physica D (2023)Show abstract
In this article we analyze several mathematical models with singularities where the classical cotangent model is replaced by a b-cotangent model. We provide physical interpretations of the singular symplectic geometry underlying in b-cotangent bundles featuring two models: the canonical (or non-twisted) model and the twisted one. The first one models systems on manifolds with boundary and the twisted model represents Hamiltonian systems where the singularity of the system is in the fiber of the bundle. The twisted cotangent model includes (for linear potentials) the case of fluids with dissipation. We relate the complexity of the fluids in terms of the Reynolds number and the (non)-existence of cotangent lift dynamics. We also discuss more general physical interpretations of the twisted and non-twisted b-symplectic models. These models offer a Hamilton- ian formulation for systems which are dissipative, extending the horizons of Hamiltonian dynamics and opening a new approach to study non-conservative systems.
[1] Baptiste Coquinot, Philip J. Morrison, A General Metriplectic Framework With Application To Dissipative Extended Magnetohydrodynamics, Journal of Plasma Physics (2020)
Show abstract
General equations for conservative yet dissipative (entropy producing) extended magnetohydrodynamics are derived from two-fluid theory. Keeping all terms generates unusual cross-effects, such as thermophoresis and a current viscosity that mixes with the usual velocity viscosity. While the Poisson bracket of the ideal version of this model has already been discovered, we determine its metriplectic counterpart that describes the dissipation. This is done using a new and general thermodynamic point of view to derive dissipative brackets, a means of derivation that is natural for understanding and creating dissipative dynamics without appealing to underlying kinetic theory orderings. Finally, the formalism is used to study dissipation in the Lagrangian variable picture where, in the context of extended magnetohydrodynamics, non-local dissipative brackets naturally emerge.